Applied Thermodynamics
Enthalpy
What is Enthalpy?
Enthalpy is a state function meaning In the thermodynamics of equilibrium, a state function, function of state, or point function for a thermodynamic system is a mathematical function relating several state variables or state quantities (that describes equilibrium states of the system) that depend only on the current equilibrium thermodynamic state of the system (e.g. gas, liquid, solid, crystal, or emulsion), not the path which the system has taken to reach its present state
Properties
Enthalpy is the sum of the system’s internal energy and the product of its pressure and volume.
- $H = E +PV$
- The energy of the gas is not just the vibration. The movement of the particles kinetically also exerts a pressure.
- Using the first law: $dh = Tds + vdp$, note specific units
- So change in specific enthalpy is change in heat plus change in pressure
Thermodynamic Equations
| Equation | Explanation | Variables |
|---|---|---|
| pV = mRT | Perfect Gas Law | p: Pressure, V: Volume, m: Mass, R: Gas Constant, T: Temperature (K) |
| $R = c_{p} - c_{v}$ | Relation between the gas constant and Cp, Cv | |
| $H = E +PV$ | Equation for Enthalpy | H: Enthalpy, E: Internal Energy, P: Pressure, V: Volume |
| $\gamma = c_{p} / c_{v}$ | Ratio of Specific heats | |
| $E = mc_{v}T$ | Internal energy is proportional to temperature for a perfect gas | |
| $dS = dQ/T$ | Change in Entropy is related to change in heat at the temperature it occurred |
Heat
- Heat is not a substance and it cannot be stored
- Heat is involved in an interaction called “heat transfer”
- “You do heat on something” like “You do work on something”
- Heat transfer to a system is positive
- Heat transfer away from a system is negative
- A process that has no heat transfer is called “adiabatic”
Laws of Thermodynamics
First Law
- Energy can not be created or destroyed.
- The change of internal energy of a system is equal to the heat transfer from the surrounding to the system minus the work done by the system on the surroundings
- $\Delta E_{0} = Q -W$
First Law of Thermodynamics (rewritten)
- $dE = TdS - pdV$, change in energy = change in entropy - change in work
Second Law
- The entropy of the universe always increases.
- In an ideal reversible process, the incremental change in entropy is the incremental heat transfer divided by the temperature at which that transfer occurs
- $dS = dQ/T$, Change in entropy is change in Heat divided by the temperature the change occurs at
- When the entropy dose not change, the process is called “isentropic”
- In reality all processes have irreversibility. For example, friction occurring in a piston is an irreversible process. The overall entropy of the universe always increases. $dS > dQ/T$
Third Law
- The lowest possible temperature is -273 Celsius or absolute zero. At this temperature there is no molecular movement and so a perfect crystal would have no disorder.
Work
- Work is a process or interaction, it cannot be stored.
- Word done on a system by its surroundings is positive work
- Work done by a system on the surroundings is negative work
- Change in work is - pressure * Volume ( $dW = pdV$)
Specific and non-specific quantities
- Many gas properties are dependant on the mass of gas involved. E, S, Q, H, V
- Hence mass-specific properties (per-unit mass) often use e, s, q, h, v. For example “specific energy”, e, j/kg
- So they are generally lowercase when specific.
- Note the specific volume of a gas, v, is the inverse of its density. $v = 1/\rho$
- However some parameters such as pressure, P, and Temperature, T, are independent of the mass of the gas.
Thermodynamic Processes
There are 4 main thermodynamic Processes:
- Isothermal
- Adiabatic
- Isobaric
- Isovolumetric
Isovolumetric Processes
Overview
Describes a system in which the volume is held constant throughout the process. This means no work can be done by the process as displacement is required as a condition to extract work.
Description
- No change in volume indicates no work can be done
Properties of Isovolumetric Processes
- $\Delta E = Q$
- W = 0
- $\Delta E = Q = mC_v\Delta T$ Change in Entropy: $s_1 - s_2 = \Delta s= c_{v}log(T_{1}/T)$
Isobaric Processes
Overview
Describes a process in which the pressure is kept constant through out. This is generally done by allowing the volume to vary throughout the process.
Description
- No change in pressure
Properties of Isobaric Processes
- $W = P\Delta V$
- $\Delta E = Q -W$
- $\Delta E = mC_v\Delta T$
- $Q = mC_p\Delta T$
Isothermal Processes
Overview
Describes a system in which there is no change in temperature and so there is also no change in Internal Energy meaning P and V must change to maintain the constant temperature condition.
Description
- No change in temperature. No change in Internal Energy so P and V change to maintain a constant temperature
Properties of Isothermal Processes
- PV = Constant, $P_1V_1 = P_2V_2$
- $\Delta E = 0$, No change in Internal Energy
- Q = W
- $W = mRT ln({V_2\over V_1})$
- $W = P_1V_1 ln({V_2\over V_1})$
- $W = P_2V_2 ln({V_2\over V_1})$
Adiabatic Processes
Overview
An adiabatic process describes a thermodynamic process that doesn’t transfer heat to or from its surroundings. This does not mean no work can be done. Energy can still flow just not in the form of heat.
Description
- No Heat transfer to or from the surroundings, nothing is held constant
Properties of Adiabatic Processes
- $pV^\gamma = const$, Therefore ${P_2 \over P_1} = ({V_1 \over V_2})^\gamma$
- Q = 0, No Heat transfer
- $W = -\Delta E$, Work is equal to the change in Internal Energy
- $\Delta E = -W$
- $W = -mC_v(T_2 - T_1)$
- $W = { C_v \over R} (P_2V_2-P_1V_1)$
Isentropic Processes
- Are a type of Adiabatic process but are also reversible
Thermodynamics of Perfect Gases
- pV = mRT, perfect gas law
- Specific Terms: $pv = RT$
- The gas constant is related to two constants: $R = c_{p} - c_{v}$
- The ratio of specific heats is: $\gamma = c_{p} / c_{v}$
- Internal energy is proportional to temp: $E = mc_{v}T$
- Enthalpy is proportional to: $H = mc_{p}T$, so in specific terms: $h=c_{p}T$
- For an isentropic process: $c_{p} {dT\over T} = R {dp\over p}$
- For isothermal process: $ds = R {dp\over p}$
Cycles
- In thermodynamics Cycles are processes that eventually return back to their initial conditions and so can repeat indefinitely.
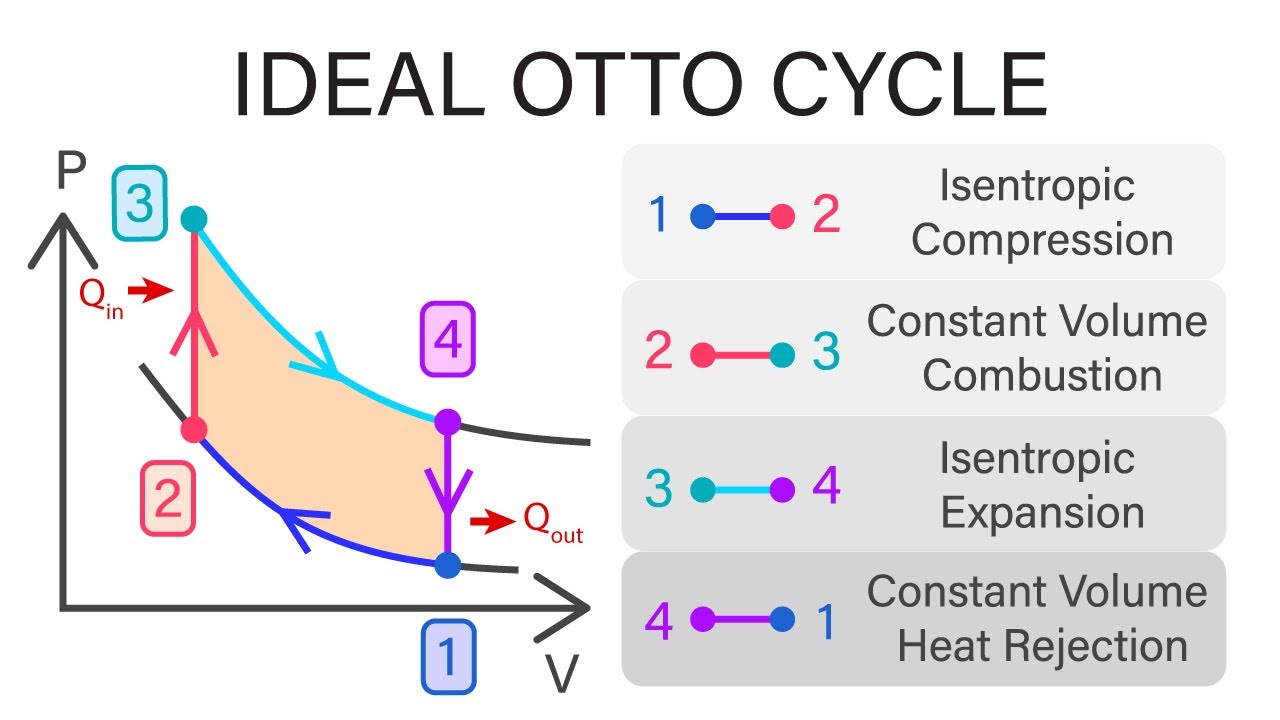
Otto Cycle
- Car engine
- Comprised of 4 Processes:
- Isentropic Compression (1-2)
- Heat transfer at constant volume (2-3) (Heating of the gas)
- Isentropic expansion to original volume (3-4)
- Heat transfer at constant volume (4-1) (Cooling the gas)
- Efficiency can be computed: $\eta = 1 - {T4 - T1 \over T3 - T2}$
Brayton Cycle
- The gas turbine cycle
- Can be made unlike the Carnot cycle
- Comprised of 4 Processes:
- Isentropic Compression (1-2)
- Isobaric Heat addition Process (Combustion) (2-3)
- Isentropic Expansion (Pressure decrease, volume increase) (3-4)
- Isentropic Expansion (4-1)
- Shown on diagram as a closed loop system, this is not true to real life.
- Efficiency can be computed: $\eta = 1 - {T4 - T1 \over T3 - T2}$
Carnot Cycle
- $W = (T_{2,3} - T_{1,4})\Delta S$
- Heat transfer from surroundings to system is: $\Delta q = T_{2,3}\Delta S$
- Heat transfer from surroundings to system is: $\Delta q = T_{1,4}\Delta S$
- Efficiency: $\eta_{cycle} = 1 - {T_{1,4}\over T_{2,3}}$